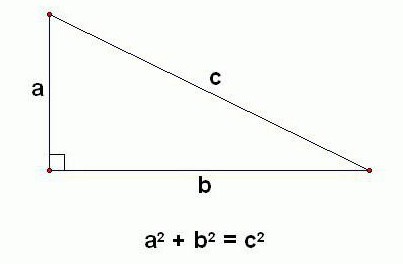
Halvkantens bisektor og dens egenskaber

Blandt mange tinggymnasiet er der som "geometri". Traditionelt menes det, at forfædrene til denne systematiske videnskab er grækerne. Hidtil kaldes græsk geometri elementær, da det er hun, der begyndte at studere de enkleste former: fly, lige, regelmæssige polygoner og trekanter. På sidstnævnte vil vi stoppe vores opmærksomhed, eller rettere på bisektoren af ​​denne figur. For dem der allerede har glemt er bisectoren i trekanten et segment af bisektoren af ​​en af ​​trekantenes vinkler, der deler den i halvdelen og forbinder vertexet til det punkt, der ligger på den modsatte side.

Bisektoren i en trekant har en række egenskaber, som du skal vide, når du løser visse problemer:

• Vinkel bisector er et geometrisk punktpunkt fjernet på lige afstande fra siderne ved siden af ​​hjørnet.
• Bisektoren i trekanten deler det modsattefra vinklen af ​​siden til segmenterne, som er proportional med de tilstødende sider. For eksempel givet trekant MKB, hvor K går fra hjørne bisector forbinder vinklens toppunkt til punktet A på den modsatte side MB. Ved at analysere denne egenskab og vores trekant har vi MA / AB = MK / KB.
• Det punkt, hvor bisektorerne i alle tre vinkler af en trekant skærer midt i en cirkel, der er indskrevet i samme trekant.
• Basis af bisektorerne af en ydre og to indvendige hjørner er på samme lige linje, forudsat at det ydre hjørnes bisektor ikke er parallel med den modsatte side af trekanten.
• Hvis to bisektorer af samme trekant er ens, er denne trekant enslig.

Det skal bemærkes, at hvis der er givet tre bisektorer, så er konstruktionen af ​​en trekant over dem, selv ved hjælp af kompas, umulig.

Meget ofte, når man løser problemer, er bisektorentrekant er ukendt, men det er nødvendigt at bestemme dens længde. For at løse et sådant problem er det nødvendigt at kende den vinkel, som bisektoren deler i halvdelen, og siderne grænser op til denne vinkel. I dette tilfælde er den ønskede længde er defineret som forholdet mellem den dobbelte hjørne tilgrænsende til produktsiden og cosinus til vinklen af ​​gennemskæring med summen af ​​sider støder op til hjørnet. For eksempel er den samme MKB trekant givet. Bisektoren strækker sig fra vinklen K og skærer den modsatte side af MB ved punkt A. Vi angiver den vinkel, fra hvilken bisektrixen forlader, y. Lad os nu skrive ned alt, hvad der er sagt i ord i form af en formel: KA = (2 * MK * KB * cos y / 2) / (MK + KB).

Hvis værdien af ​​den vinkel, hvorfrabisector af trekanten, er ukendt, men kendt af alle sine sider, for at beregne længden af ​​bisector, vil vi bruge en ekstra variabel, som vi kalder semiperimeter og betegnet med bogstavet P: P = 1/2 * (MK + KB + MB). Derefter foretage nogle ændringer i den ovennævnte formel, som bestemmes ved vinkelhalveringslinien af ​​længden, nemlig i tælleren sat to gange kvadratroden af ​​produktet af længden af ​​siderne støder op til hjørnet, særlig semiperimeter hvor semiperimeter trækkes fra længden af ​​den tredje side. Vi forlader nævneren uændret. I formel formular vil dette fremstå som: KA = 2 * √ (MK * KB * P * (P-MB)) / (MK + KB).

Bisektoren i en retvinklet trekant harAlle de samme egenskaber som i det almindelige. Men i tillæg til det allerede kendte er der også en ny: bisektorerne af de akutte vinkler af en retvinklet trekant udgør en vinkel på 45 grader ved krydset. Om nødvendigt er det let at bevise at bruge egenskaberne af en trekant og tilstødende vinkler.

Bisektoren af ​​en ensartet trekant sammen medhar flere egenskaber til fælles. Lad os huske, hvilken slags trekant det er. I en sådan trekant er de to sider ens, og vinklerne ved siden af ​​bunden er ens. Følgelig følger det, at bisektorer, der falder ned til siderne af en enslig trekant, er lig med hinanden. Desuden er bisektoren, sænket til basen, både højde og median.